NGBoost, 예측의 불확실성을 고려한 Boosting 모델

in DATA on Machine Learning


Introduction

NGBoost에 대해 알아보기 위해서는 Boosting 대표적인 모델인 XGBoost가 빠질 수 없겠죠?

Random Forest는 각 Tree 모델을 독립적으로 만드는 모델입니다. 반면 Boosting은 순차적으로 Tree 모델을 만들어 이전 Tree 모델로부터 더 나은 Tree 모델을 만들어내는 알고리즘입니다. Boosting 알고리즘은 Tree 모델을 기반으로 한 알고리즘으로, Random Forest보다 훨씬 빠른 속도와 더 좋은 예측 능력을 보여줍니다.

이에 속하는 대표적인 모델로 XGBoost가 있으며, XGBoost(eXtra Gradient Boost)는 GBM에서 파생된 Tree 모델 기반의 앙상블 학습 방법입니다. Kaggle 대회에서 상위를 차지한 많은 Top Ranker들이 사용하는 성능이 검증된 Boosting 모델이며, XGBoost 이후 다양한 부스팅 모델이 나왔지만 아직까지 많은 사람들이 CatBoost, LightGBM과 함께 XGBoost를 사용하고 있습니다. 그만큼 인기 있고 대중적인 모델이라 하이퍼파라미터 튜닝, 실제 활용 예시 등 수많은 참고 자료가 존재합니다. 실제로 저도 간단하게 데이터를 확인하기 위해서 퀵하게 XGBoost를 사용해서 검증하기도 하구요!


NGBoost (Natural Gradient Boost)도 마찬가지로 GBM 기반의 알고리즘이고, Andrew Ng 교수가 속해 있는 스탠퍼드 대학의 ML Group 연구소에서 2019년 10월 9일에 제안한 새로운 Boosting 알고리즘입니다. XGBoost와 LightGBM 위주로 모델링을 진행 하고 있었는데, 최근에 분산(variance)을 구하여 불확실성(uncertainty)를 측정할 수 있는 Boosting 알고리즘 관련하여 구글 검색을 하던 중 NGBoost를 발견하여 공부할 겸 소개해보고자 해당 포스팅을 작성하게 되었습니다.
NGBoost는 Probabilistic Gradient Boost 기법을 사용하는 확률론적 예측 알고리즘이라고 하는데, 어떤 의미일까요? 지금부터 한번 파헤쳐 보도록 하겠습니다😎


1. NGBoost란?

제가 앞서, NGBoost는 확률론적 예측 알고리즘이라고 말씀드렸는데요! 간단하게 말하자면, 예측 결과값을 제공할 때 이에 대한 확률 분포 또한 제공하는 것입니다.

기존 회귀(regression) 모델은 특정 데이터들이 들어왔을 때 하나의 y에 대한 예측(점 추정치)하는 것에 초점을 두고 있는 것에 반면, NGBoost는 해당 점에 대한 분포를 반환하여 데이터 대한 전체 확률 분포를 찾는 것을 목표로 하고 있습니다.

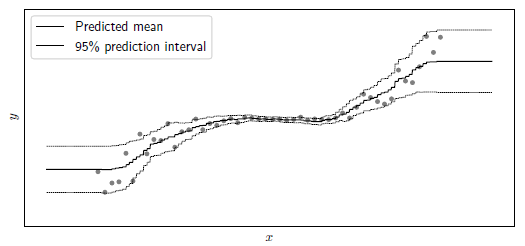
아래 그림을 예시로 들자면, NGBoost의 목표는 각 x지점에서 각각 다른 평균과 분산을 추정하여 데이터에 대한 전체 확률 분포를 찾는 것입니다. (확률적 예측을 가능하게 하고자 함)

  • 두꺼운 선 : 예측값의 평균(predicted mean)
  • 가는 선 : 95% 확률 예측 구간(95% prediction interval)
    • 가는 선 사이에 예측값이 있을 확률이 95% 이상임을 의미

즉, 확률 분포를 구하기 위해, 각 데이터의 Input 별로 해당 값을 가장 잘 설명하는 파라미터(=여기에서는 평균과 분산을 의미)를 찾는 알고리즘이 바로 NGBoost입니다.

  • 확률적인 방법을 사용하여 예측 모델의 불확실성을 추정하고, 이를 통해 예측 결과의 신뢰도를 제공


2. NGBoost 구성

✨ 핵심 아이디어

NGBoost는 Multiparameter distributional boosting과 Natural gradient update 를 활용합니다.

  1. 우선 Loss function과 유사한 역할을 하는 Scoring rule을 선정합니다.
    • 이때, P(YㅣX=x)가 특정 parametric form을 따른다고 가정합니다.
  2. 이 때 필요한 파라미터인 μ(X)와 σ(X)를 추정하기 위하여 Natural Gradient을 활용하게 됩니다.
    • Gradient Boosting은 평균과 분산 값에 대한 파라미터 추정이 명확하게 되지 안흐므로, Natural Gradient 방식을 활용하여 실제 최적값에 도달하도록 합니다.
    • Gradient Descent의 parameter search space에 대한 조정을 진행하여 새로운 공간 상에서 gradient 값과 방향에 대한 탐색을 진행하게 됩니다.
  3. Boosting 알고리즘을 여러번 반복하면서 해당 파라미터들 값들을 동시에 업데이트 시킵니다.
    • 각각의 Boosting Step에서 샘플링된 가중치와 알고리즘의 파라미터에 대한 분포를 추정하여, 해당 분포를 기반으로 예측 모델을 개선하고 불확실성을 고려한 예측을 수행하게 됩니다.


📌 NGBoost 구성

아래의 방법으로 구성되어있으며, 각 구성에 대해 간단히 설명을 진행하도록 하겠습니다.

우선, NGBoost는 위의 그림과 같이 Base Learners, Probability Distribution, Scoring Rule로 구성되어 있습니다.

1️⃣ Base Learner

  • NGBoost는 Gredient Boosting과 유사하게 기본 모델을 사용하여 예측 모델을 구축합니다.
  • 가장 기본적인 학습기는 결정트리(Decision Tree)입니다.

2️⃣ Probability Distribution

  • Input을 받아 Base Learner로 예측한 결과를 활용하여 확률 분포를 만듭니다.
  • 확률 분포는 Target Value의 타입에 따라 바뀔 것입니다.
    • 일상생활에 대한 값이라면 정규 분포를, Binary값이라면 베르누이 분포를 따르게 됩니다.

3️⃣ Scoring Rule

  • 파라미터를 학습하기 위해서는 적합한 scoring 함수가 정의되어야 하며, 예측한 확률 분포와 실제 Target Value를 토대로 성능 측정을 합니다.
    • 예측에 사용할 확률분포 함수 P가 주어졌을 때, 하나의 관측치 y에 대한 scoring 함수가 필요합니다. → S(P, y)
    • 또한 Q를 y에 관한 정답 분포라고 했을 때, 이에 대한 scoring 함수도 필요합니다. → S(Q, y)
    • 위와 같이 두 함수를 정의하면 아래의 수식이 만족되어야 하며, 수식이 의미하는 바는 적합한 scoring 함수라면, 정답 분포(Q)의 점수 값의 기댓값은 예측 분포(P)의 점수 값의 기댓값보다는 항상 적게 설계되어야 한다는 것입니다.
    • 그렇기 때문에, scoring 함수는 고정된 P가 아니라 찾고자 하는 파라미터 θ에 관한 S(θ, y)라고 할 수 있습니다.
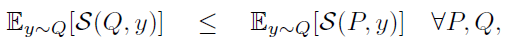
  • 논문에서는 성능 측정을 위한 scoring 함수로 MLE(Maximum Likelihood Estimation)과 Continuous Ranked Probability Score(CRPS)를 제시합니다.
    • MLE
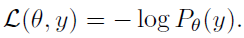
      • 일반적으로 사용되고 있는 방법이며, maximum likelihood를 이용한 scoring 함수입니다.
    • CRPS
      • MLE 보다 robust하다고 알려진 scoring 함수입니다.
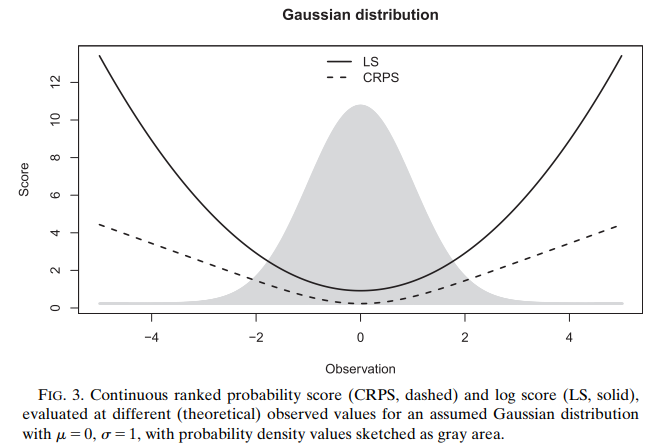
      • MLE의 문제점은 log함수를 사용하므로 예상 값과 관측치와의 차이가 많이 날수록 score 값이 급격하게 상승하는 문제점이 있습니다. 이런 문제점을 방지하고자, CRPS를 이용하여 관측치가 평균보다 멀어질 때 보다 완만하게 score 값이 증가하는 것을 반영하고자 했습니다.
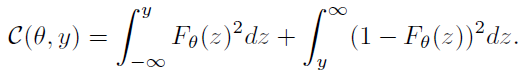
      • 아래의 그림을 보면, CRPS가 극단값 부분에서 MLE에 비해 score 값이 상대적으로 낮음을 확인할 수 있습니다.

위 단계를 반복하며 성능을 높여가게 되는데, 이때 수식에서 Fit Natural Gradient라고 쓰여져있는 것을 확인할 수 있습니다. 일반적으로 알고 있는 gradient descent 방법에서 왜 Natural이 붙여지게 되었을까요? 그 이유는 파라미터가 일반적으로 gradient에 사용하는 distance에서 얻은 결과가 아닌 분포에서 얻은 것이기 때문입니다. 따라서 논문에서는 ∇ 대신 위에 ~가 표시되어 있는 것을 확인할 수 있습니다.

💡 Natural Grdient

  • 일반적인 Gradient(스텝 사이즈가 일정한 크기를 갖는)와 달리, Natural Gradient는 파라미터의 불변성(invariance)을 고려하여 스케일링된 그레이디언트를 사용합니다.
  • 일반적인 Gradient는 파라미터 공간에서 일정한 크기의 스텝을 이동하며 최적점을 찾아가는 방식입니다. 그러나 파라미터의 스케일이 서로 다른 경우, 스케일이 큰 파라미터는 작은 파라미터보다 더 큰 영향을 미칠 수 있습니다. 이는 Gradient의 방향을 왜곡시킬 수 있고, 최적점에 수렴하는 데 불필요한 시간을 소요할 수 있습니다.
  • Natural Gradient는 Loss값에 대한 미분으로 얻은 gradient를 업데이트 한다고 해서(Loss를 minimize하는 gradient), 업데이트 된 분포가 과연 더 좋은 분포인가에 대한 의문에서 출발하였습니다.
    • 파라미터 공간에서 유클리디안 척도를 사용했을 때에 발생하는 문제는 다음과 같습니다.
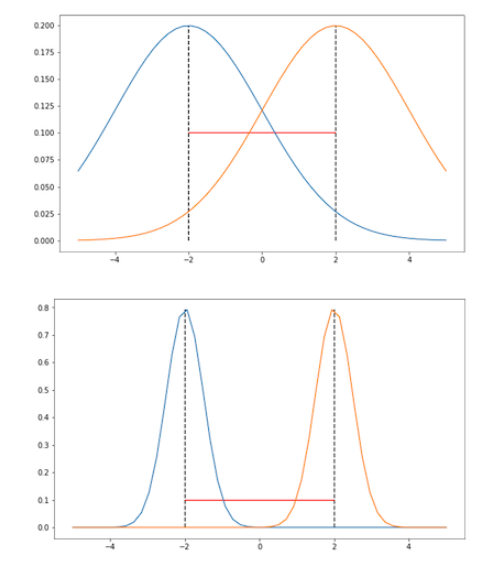
      • 분산이 고정되어 있고 오직 평균만 파라미터화된 가우시안 분포를 가정합시다.
      • 두 분포의 평균은 두 그림에서 모두 같지만, 분산은 서로 다릅니다. 분명하게 위 그림보다 아래 그림에서 분포의 차이가 더 크다는 것을 알 수 있습니다.
      • 하지만 분포의 거리를 유클리디안 거리로 사용한다면, 위 그림과 아래 그림에서 두 분포의 거리는 같습니다. 따라서 오직 파라미터 공간에서만 두 분포를 바라본다면, 이 파라미터들로 만들어지는 분포 간의 정보를 상당 부분 잃게 됩니다.
  • 그렇기 때문에 Natural Gradient는 이러한 의문 해결하기 위해, 파라미터 공간이 아닌 분포 공간에서 가장 가파른 경사를 택하여 step을 취하는 방법을 사용합니다. 파라미터의 분포 공간에 대한 정보를 활용하여 Gradient를 스케일링합니다. 이를 통해 각 파라미터의 스케일에 맞추어 적절한 크기로 이동하여 최적점을 탐색할 수 있습니다.
    • 즉, Natural Gradient를 사용하면 파라미터의 불변성을 보장하면서 효율적인 최적화를 수행할 수 있습니다.
  • 이러한 이유로 파라미터 공간이 아닌 분포 공간에서 step을 취하는 방법을 ‘자연스럽다’라고 붙임으로써, Natural Gradien Descent 방법이라 부릅니다.

4️⃣ Parameters Update

위 3가지 단계를 반복하면서, 각 데이터에 해당하는 parameter θ는 다음과 같은 알고리즘으로 학습되어 얻을 수 있습니다. (여기서는 θ = (μ, log σ) 입니다. )
알고리즘을 보면, ρ라는 m번째 반복 시점에 대한 scaling factors를 사용하여 얻고자 하는 θ값을 조절하게 됩니다. 또한 작은 lr 값(실험에서는 0.1, 0.01을 사용)을 추가적으로 곱하여 사용하였습니다.


3. NGBoost Experiments

📊 학습 시각화

위에 해당하는 그림은 일반적인 gradient를 사용한 결과이고, 아래에 해당하는 그림은 natural gradient를 사용한 결과입니다. 가운데의 진한 선이 평균에 해당하는 부분이며, 위에 그림은 평균값이 고정된 반면(가로의 선으로 되어있음), 아래 그림은 fitting 후 평균 또한 변하여(곡선의 선으로 되어 있음) 보다 끝이 곡선으로 이루어진 구간 추정의 결과를 얻을 수 있습니다.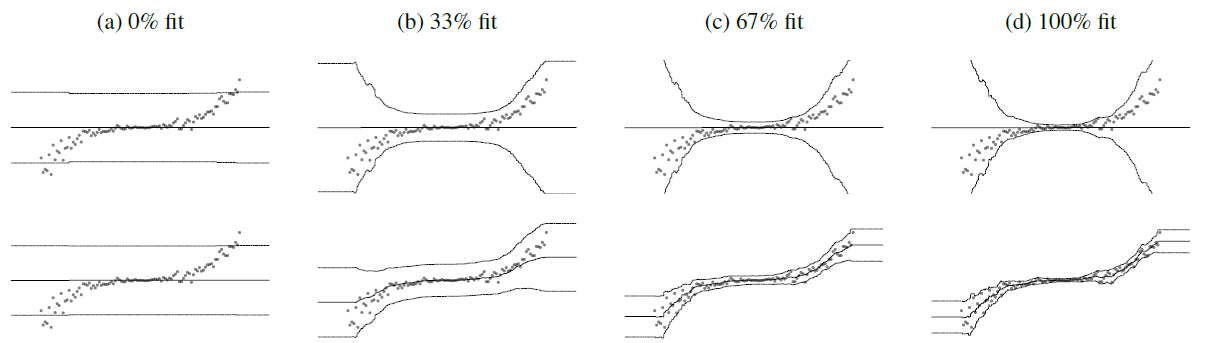

📈 점 추정 & 구간 추정

1. 점 추정

점 추정에서는 NGBoost가 좋은 결과를 얻지만, Gradient Boosting 모델이 조금 더 좋은 결과가 나오는 것을 확인할 수 있습니다.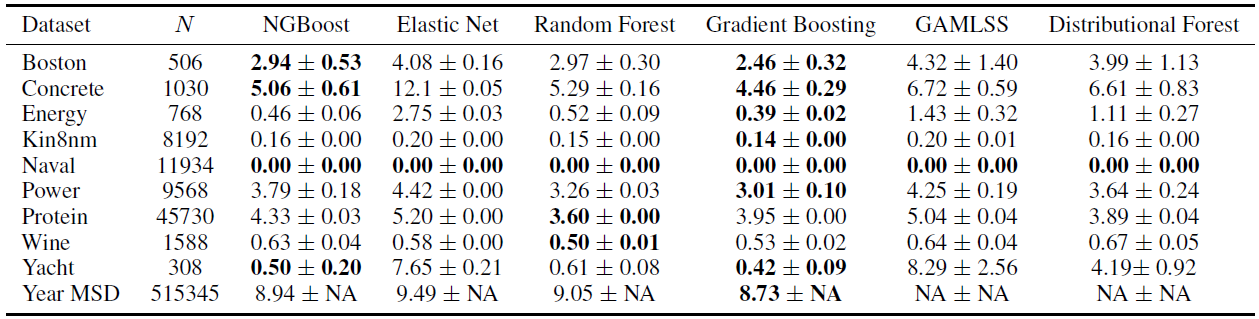

2. 구간 추정

구간 추정에서는 NGBoost가 거의 모든 데이터에 대하여 가장 좋거나 준수한 추정을 한다는 것을 확인할 수 있습니다.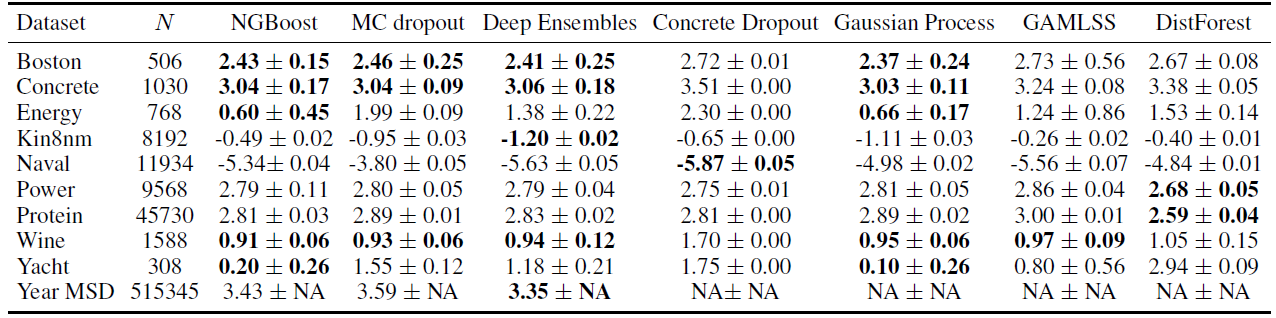


4. XGBoost vs. NGBoost

XGBoost 모델과 NGBoost 모델은 각각의 특징과 장단점을 가지고 있으며, 무조건적으로 특정 모델이 좋다고 할 수 없습니다. 실제 성능 및 사용 사례에는 다양한 요소가 영향을 미치기 때문입니다. 그렇기 때문에 주어진 문제에 가장 적합한 성능과 요구사항 충족을 목표로 잡은 다음, 해결해야 하는 문제에 맞는 실험 및 비교를 통해 XGBoost와 NGBoost의 성능을 평가하여 모델을 선택해야 합니다.
XGBoost와 NGBoost를 비교한 일반적인 차이점은 다음과 같습니다.

1️⃣ 불확실성 추정

  • XGBoost : 일반적인 Boosting 알고리즘으로, 불확실성 추정을 제공하지 않습니다.
  • NGBoost : 확률적인 방법을 사용하여 예측 모델의 불확실성을 추정하며, 예측 분포를 통해 신뢰 구간 등의 정보를 제공합니다.

2️⃣ Feature Selection

  • XGBoost : 변수 중요도를 계산하여 Feature Selection을 수행합니다.
  • NGBoost : NGBoost 또한 변수 중요도를 계산하여 Feature Selection을 수행합니다.

3️⃣모델 해석성

  • XGBoost : 예측 결과에 대한 해석성이 상대적으로 떨어집니다.
  • NGBoost : 확률적인 예측과 사후 분포 추정을 통해 모델의 예측 결과를 해석하는데 도움이 됩니다.

4️⃣ 계산 속도

  • XGBoost : 빠른 계산 속도와 높은 효율성을 가지고 있습니다.
  • NGBoost : 확률론적인 방법을 사용하므로 계산 속도가 상대적으로 느립니다.

NGBoost의 대표적이면서 가장 큰 특징은 바로 확률적 예측이 가능하다는 것입니다. (예측의 불확실성에 대한 측정값 제공) 예측은 언제나 불확실성을 내포하기 때문에, 모델의 예측값에 대한 불확실성을 측정하여 확률 분포를 보고자 할 때 NGBoost가 매우 유용할 것으로 생각됩니다.

아래는 그에 대한 예시입니다.

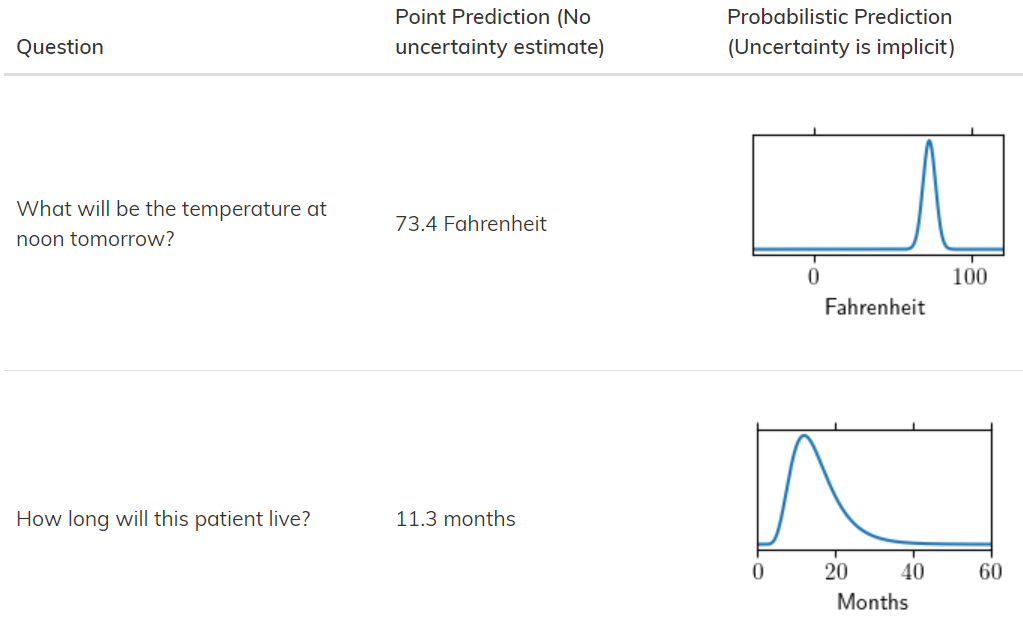
NGBoost는 Question에 대한 Point Prediction 뿐만 아니라 Probabilisitc Prediction을 보여줍니다. ‘내일 날씨가 몇 도 이냐?’ 에 대한 질문에 73.4일 확률을 표시합니다.

Conclusion

NGBoost를 접하고 논문을 읽을 때, Natural Gradient라는 방식에 대해 처음 접하여 수식들이 꽤나 생소했습니다.😂 하지만 기존 모델들의 단점을 해결하기 위하여, 새로운 아이디어를 제안하여 접목시킨 것을 보며 매우 재미있는 모델이라는 생각이 들었습니다.
역시.. 다양한 방면으로 생각하고 적용하는 자세가 무척 중요한 것 같습니다! 다시 한번 깨닫게 되네요!
사용된 사례도 많지 않아 조금 더 공부를 해야겠지만, 실무에서도 요긴하게 쓰일 수 있을 것 같아 기대가 됩니다. 다음 포스팅에는 많이 알려진 데이터를 하나 선정하여, 어떤 알고리즘이 더 우수한지 비교해보고자 합니다.


NGBoost를 아래와 요약하자면 다음과 같습니다.

  • NGBoost는 확률 분포를 반환하는 새로운 Boosting 알고리즘
  • 일반적인 Gradient 방법이 아닌 Natural Gradient 방법을 적용하여, 파라미터 공간에서의 Gradient를 보다 효율적으로 계산하고 사용
    • Parametrization에 invariant한 Natural Gradient를 도입해서 Multiparameter Boosting을 가능하게 함
  • NGBoost는 예측 모델에 대한 불확실성을 제공하기 위해 확률적인 방법을 사용
    • X가 주어졌을 때의 확률분포를 구성하는 파라미터의 추정을 통해 확률적 예측을 가능하게 함
      • 어떤 분포를 가정하더라도 가능하다는 장점이 존재하며, Prior의 분포를 안다고 가정할 때 y의 분포를 제한해서 학습 가능
    • 이는 예측값의 신뢰도를 평가하고 예측의 불확실성을 고려할 수 있는 장점을 제공 (ex. 예측 구간에 대한 신뢰 구간)
  • 다른 Probailistic Prediction 기법들과 비교하여, 빠르고 / 유연하고(=분포가정) / 성능이 나쁘지 않음

Reference




© 2020.02. by ysjang0926

Powered by theorydb